Три любимых несложных задачки
![]()
Надо
сказать, что эпизодически оказывался я в составе разного
рода экзаменационных комиссий, обычно подменял кого-то в
разовом порядке.
И были у меня три любимых задачки, все достаточно простые и
не требующие ничего, кроме простой арифметики.
Однако сыпались многие.
![]()
Есть
в графском парке темный пруд...
Он потихоньку зарастает ряской, каждый день заросшая
площадь удваивается.
Весь пруд зарос за 64 дня.
За сколько дней заросла четверть пруда?
Доля
достаточно быстро ответивших: 16 дней
– доходит до
50%.
Говоришь им, что это неправильный ответ, – ступор.
Трудно укладывается в голове показательная функция,
линейная-то куда естественней!
Начинаешь объяснять: ну всё же просто! Весь пруд за 64,
значит, половина пруда... нет, не за 32, а за 63!
(Искреннее удивление в глазах). А четверть – за 62 дня.
Кивают, но понимания в глазах не прибавляется.
Правда, не могу не сказать, что довольно многие всё же сразу
отвечают правильно,
да ещё и удивляются: что, мол, так просто-то? Многие, да. Но
не все.
![]()
У Белкина задача "про клюкву" – просто атас! (подслушанный разговор абитуриентов)
Старинная задачка чуть ли не из Магницкого.
Мужик вёз на базар сто пудов клюквы влажностью 99%.
Ясное дело: клюква
– почти одна
вода.
В дороге клюква немного подсохла, теперь её влажность всего
98%.
Сколько ж пудов мужик привез на базар?
Простенькая задачка в два действия. Третьеклассник,
покумекав, решает ее на раз.
Но за последующие школьные годы способность покумекать
несколько, гм, подсохла. Почти как клюква...
Число сразу отвечающих: 99 пудов
– неприлично
зашкаливает.
Узнав, что это неверно, очень многие выпаливают: 98 – опять
мимо!
Начинают возню с пропорцией (годный, но длинный путь),
путаются в расчётах.
Беда и в том, что сущность процентов не понимают, полагают,
что это что-то вроде размерности.
Ладно, следите за рукой.
99% влажности
– значит, 99
пудов воды и пуд сухого остатка.
От усыхания количество сухого остатка не меняется – 1
пуд.
Но теперь этот пуд – уже 2% от общего веса.
Вот и ответ: мужик привез на базар 50 пудов.
Практически никто поверить не может. Чистый нокаут.
![]()
Третья задача потрудней, хотя тоже фактически в два действия.
Три носильщика несут за углы плоскую однородную треугольную
пластинку с углами в 30, 60 и 90 градусов.
Кому из них тяжелее всего?
Я еще не встречал человека, который бы сходу дал правильный
ответ.
Начинают рассуждать о том, что вершина прямого угла ближе
всего к центру тяжести...
И что? А вершина острого
– дальше
всего...
И что?
Однажды я даже поставил эту задачку на тренировке нашего
клуба – как вопрос "Своей игры".
Трое последовательно перечислили три угла, четвертый
растерянно промолчал.
Между тем задачка элементарна, надо только помнить, что
центр тяжести лежит в точке пересечения медиан,
а сама эта точка делит каждую из медиан в пропорции 2:1.
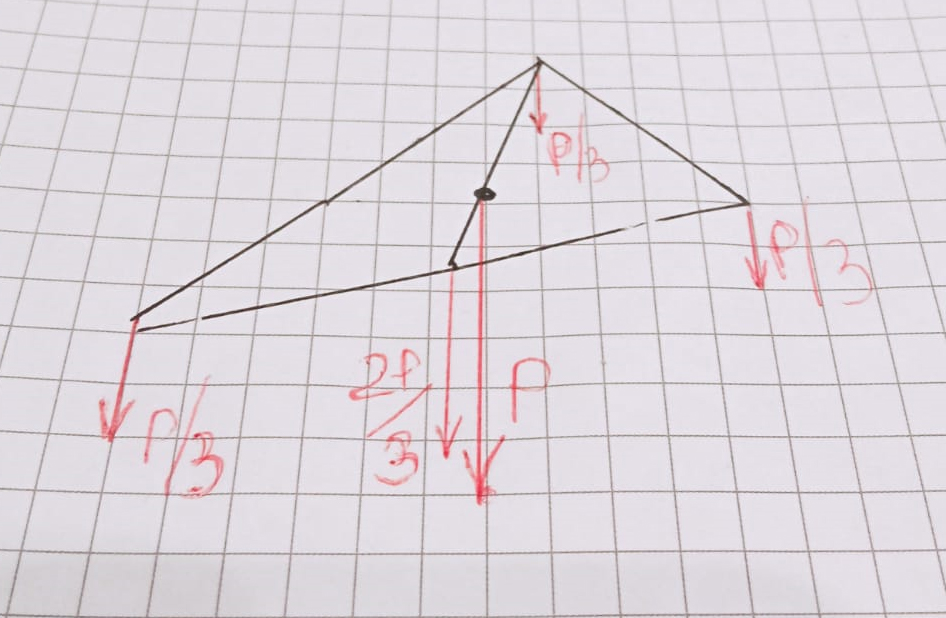
Буквой Р здесь обозначена сила тяжести. Разложим ее вдоль
медианы на две параллельные составляющие:
в середине гипотенузы это 2Р/3 и в противолежащей вершине
– Р/3.
Теперь разложим 2Р/3 вдоль гипотенузы – вуаля! В каждой
вершине Р/3.
Им всем одинаково тяжело!
Самое забавное, что решение вообще не зависит от углов – всегда получается одинаково.
Надеюсь, больше вас на эти шуточки никто не купит.
Но у экзаменатора такого добра много.
